The Monochromatic Laser

Photon Absorption

The fundamental phenomenon that enables precise control, cooling, and trapping of neutral atoms is the excitation of bound electrons through the absorption of photons. As discussed previously, exciting an electron to a higher energy state requires the absorption of a photon within a very specific range of frequencies/energies. This range is known as the line width of an atomic transition.

A discussion of the line width of atomic transitions is ubiquitous in atomic physics texts, such as C.J. Foot or Vasant Natarajan. In essence, these derivations show how the transition rate of an atom varies with respect to the frequency of incident light, which is typically a Lorentzian distribution centered at the resonant frequency of the transition.

Following this, typical treatments of the radiation pressure force (the ‘pressure’ exerted on an atom by the absorption and emission of incident photons) tend to assume that the frequency of incident light can be tuned arbitrarily close to this resonant frequency, so that the transition rate is maximized. However, in practice, it is exceedingly difficult to create a light source that is truly monochromatic, i.e. that emits a single stable frequency of light.

The most common form of light source used in magneto-optical trapping is the laser, as they are coherent sources of photons and are spatially precise. There are many variants of lasers, e.g. diode lasers, gas lasers, diode-pumped solid-state lasers, and so on. All of these variants are subject to frequency drift, i.e. the frequency of photons that these lasers emit changes stochastically as a function of time due to random fluctuations.

A popular choice in the construction of MOTs is the diode laser, as they are relatively inexpensive, and the process of stabilizing their emitted frequency is well-studied. In particular, diode lasers are often stabilized with the addition of an external cavity and a diffraction grating that allows for the fine-tuning of the output frequency of light so that the laser can remain within the line width of the desired atomic transition. These apparatus are known as external cavity diode lasers (ECDL), and are arguably the most common tools in an atomic physics lab.

External Cavity Diode Lasers

Optical Configurations

Littrow ECDL

There are a variety of configurations for external cavity diode lasers presented in the literature. The simplest, and thus most common, is the Littrow ECDL, depicted in the figure below. The laser diode is directed at a blazed diffraction grating (e.g. Thorlabs GR13-0608, $70) in the external cavity, which diffracts the light and thus alters its wavelength.

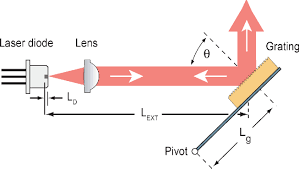
In particular, the wavelength of light after diffraction is given by the well-known optical equation:

\[n \lambda = d(\sin \theta + \sin \theta')\]

where \(n\) is the order of diffraction, \(\lambda\) is the diffracted wavelength, \(d\) is the grating constant (distance between grooves), \(\theta\) is incident angle of the diode with respect to the diffraction grating (i.e. the angle with the unit normal of the grating), and \(\theta'\) is exit angle of the diffracted beam.

In the Littrow ECDL configuration, \(\theta = \theta'\), so this reduces to:

\[n \lambda = 2d \sin \theta\]

The motivation for such a configuration is due to the nature of stimulated emission of photons. In particular, when we direct our laser diode at the blazed diffraction grating at some angle \(\theta\), thereby generating first-order diffracted light at a wavelength \(\lambda\), some of that diffracted light will be reflected back into the diode. Within the gain medium of the diode, that diffracted light will serve to amplify the emission of light at the diffracted wavelength. Therefore, if we want our laser to output light sharply peaked at some wavelength \(\lambda^\ast\), we simply mount the diffraction grating at an incident angle of \(\theta^\ast = \arcsin \frac{\lambda^\ast}{2d}\), which will amplify the emission of light at the wavelength \(\lambda^\ast\) as desired.

To control the incident angle onto the diffraction grating, we use a piezoelectric actuator (e.g. Thorlabs PK4FA2P1, $52) mounted behind a lever arm, which holds the grating. As the actuator expands, it pushes the lever arm, changing the diffraction angle slightly. An actuator with a maximum travel length of \(10 \mu m\) to \(20 \mu m\) is generally sufficient to sweep through the range of angles that will allow an experimentalist to lock the output of their ECDL to the desired frequency.

For rubidium-87, the canonical ‘cooling transition’ has a resonant wavelength of \(780.241209\) nm (in vacuum). Therefore, if we had a grating with 1800 grooves per mm, and wanted to be exactly on resonance, we would choose:

\[\theta = \arcsin \frac{780.241209 \text{nm}}{\frac{2}{1800} \text{grooves/mm}} = 44.6031975^\circ\]

Additionally, as depicted in the Littrow diagram above, the output beam of the diode must be collimated as it is emitted, via some beam limiting device (e.g. Laser-Makers 16mm beam collimator, $10). This is because most laser diodes produce inherently divergent beams, and too much power would be lost from this beam divergence to eventually be useful downstream in the experiment.

One disadvantage specific to the Littrow ECDL is that the output beam direction varies as the frequency is tuned. For tasks requiring highly precise beam alignment, this may have unwanted consequences in the downstream application. A similar configuration using a blazed diffraction grating known as the Littman-Metcalf ECDL obviates this issue by using a rotating mirror to select the output frequency (rather than rotating the grating itself). However, this configuration suffers from a relatively low power output as compared to the Littrow configuration.

Stabilization and Electronics

Recall that to cool an atom, we need to tune the frequnecy of the laser to a specific value just below the resonant frequency of its atomic transition energy. For any given atomic transition, there is an associated parameter called the line width, which tells us what range of frequencies the atom will ‘accept’ when it is to be excited. For the majority of atomic transitions, this line width is in the MHz range, which means that the wavelength of the laser must be stabilized to the sub-picometer level!

To control the ECDL in the configuration proposed above, three drivers are required: a current driver for the laser diode, a temperature controller for the Peltier device and temperature sensor, and a voltage controller for the piezo actuator.

Traditional off-the-shelf laser diode drivers are typically insufficient for controlling an ECDL; this is because they have too much noise in their output current, which in turn would correspond to fluctuations in the output wavelength of the diode due to various factors (gain profile, thermal gradients, etc). As a general rule of thumb, an ECDL current driver should be stable to 0.1uA, an ECDL temperature controller should be able to stabilize the temperature within 0.01° C of a setpoint, and an ECDL piezo driver should be stable to 100uV.

Circuit schematics and control codes for such devices are given on the main site for this project. The devices I’ve designed are digital (using a Teensy 3.5 microcontroller), which allows for end-to-end data collection and feedback on the same device.

Temperature Control

A key aspect to proper ECDL operation is precise control of the temperature of the laser diode. The wavelength of light that is output by a laser diode changes with respect to temperature (as thermal fluctuations will change the length of the internal cavity of the diode). As more current is provided to the laser diode, the temperature will rise, thereby changing the wavelength and possibly disrupting the experiment.

Thus, ECDLs are generally assembled with some form of cooling mechanism, such as a Peltier device (a.k.a. thermoelectric cooler, e.g. CUI Devices CP60231H, $20). When used in conjunction with a thermally conductive mounting apparatus for the diode, as well as some form of heatsink, a Peltier device is able to transfer heat away from the diode.

To keep the temperature stable about a set value, experimentalists often use analog circuits, in which temperature measurements are taken by an analog sensor (e.g. Analog Devices AD590, $15), and used in conjunction with a proportional–integral–derivative loop to adjust the input current to the Peltier device such that temperature remains constant.

Fine-Tuning Frequency

The fine-tuning of the frequency is achieved by adjusting the angle of incidence of the laser beam on the diffraction. In the Littrow ECDL, this is implemented by using a piezoelectric actuator to push on a flexure arm, causing it to bend ever so slightly. To tune the frequency to the desired value, we must be able to adjust the angle down to at least the hundred-thousanth of a degree. Thus, depending on the length of your flexure arm, this requires control of the actuator down to the sub-nanometer range.

Fortunately, piezoelectric actuators (particularly those made of stacks of PZT, or lead zirconium titanate) are capable of such accuracy. The piezo actuator that I use in my ECDL is a Thorlabs PK4FA2P1, which has a maximum stroke length of 9.5um when driven with 150V. Although piezos are not necessarily linear devices (i.e. the relationship between displacement and voltage is not necessarily linear), we can assume a linear relationship just for the purposes of roughly computing the step resolution of the device: if the actuator expands by 9.5um at 150V, then every 1mV step in driving voltage should correspond to a 63 picometer step in the output displacement!

Limiting noise in the piezo driver is very important - any noise in the voltage being provided to the actuator will manifest as vibrations in the ECDL, which will then cause fluctuations in the output wavelength. Moreover, piezoelectric materials are highly susceptible to material creep, meaning that even when they are driven with constant voltage, their length will vary over time. Therefore, the voltage needs to be constantly adjusted based on an external error signal (typically generated by a technique called saturated absorption spectroscopy, to be discussed below).

Optical Isolator

As discussed previously, the mechanics of an ECDL necessarily depends on the nature of stimulated emission; specifically, the fact that light reflected back into the diode can stimulate a higher level of emission at a desired wavelength. However, this effect can also backfire, if light reflected back into the diode is not of the desired wavelength. Without proper precautions, this phenomenon can easily occur in experiments, as the light emitted by the ECDL is reflected by other optical elements in the experiment.

The typical solution to this problem is to utilize an optical isolator in conjunction with the light output from the ECDL. An optical isolator is an optical element that makes use of the physical phenomenon of Faraday rotation, or the rotation of the polarization of light within certain nonlinear crystals.

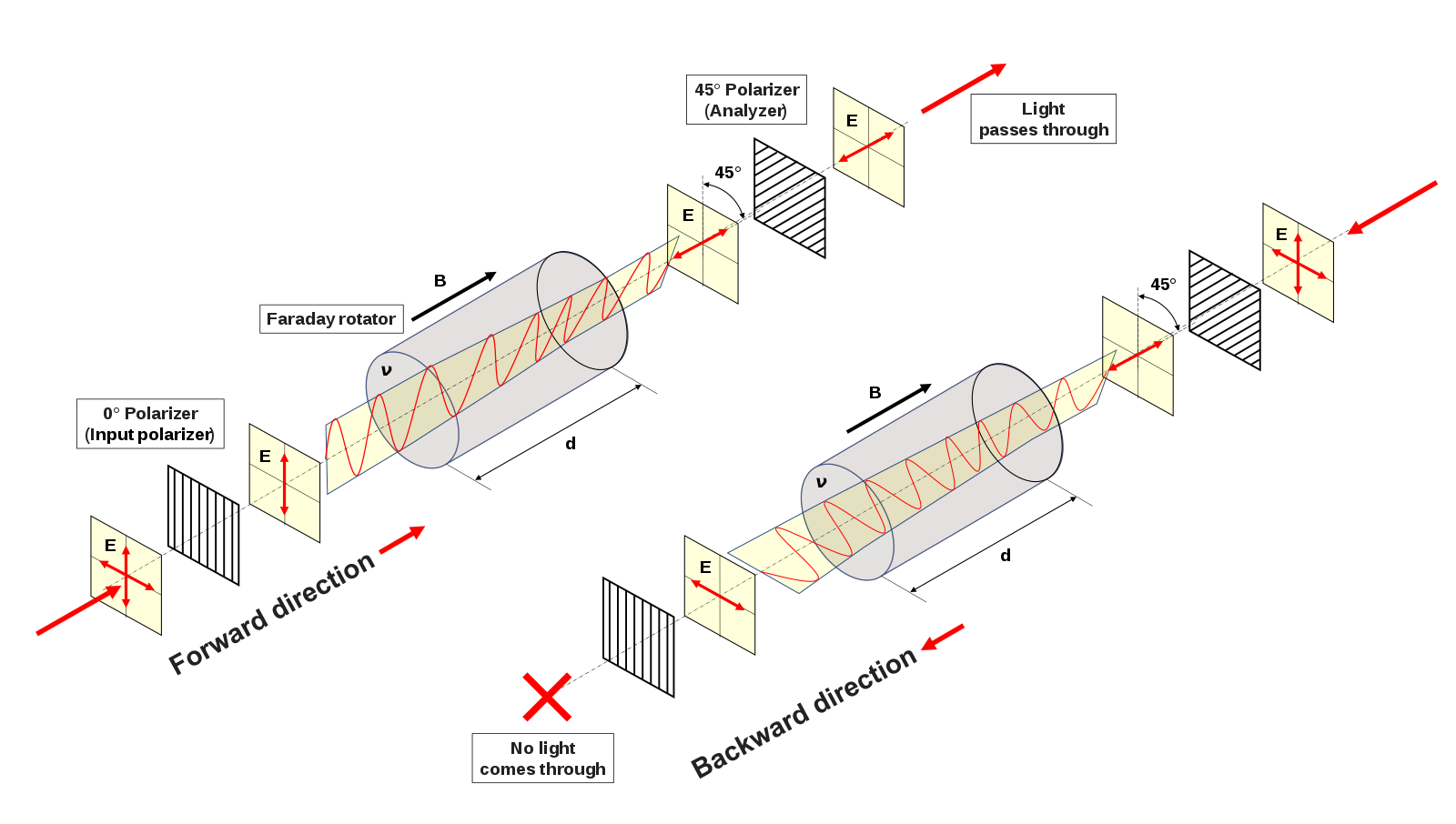
Such crystals are characterized by their Verdet constant, which is a measure of how many radians the polarization of incident light is rotated by, per meter, per Tesla. A Faraday rotator is built by placing a nonlinear crystal within a region of axial magnetic flux; as the light passes through this region, its polarization will be rotated by an angle given by:

\[\Delta \theta = V \beta L,\]

where \(V\) is the Verdet constant of the crystal, \(\beta\) is the axial magnitude flux in the crystal, and \(L\) is the length of the crystal. To create an optical isolator, then, we first place a linear polarizer (e.g. Melles Griot 03FPG009, $35) in front of such a Faraday rotator. This ensures that the light entering the Faraday rotator is uniformly polarized. Subsequently, we add a 45° polarizer (a.k.a. analyzer) after the rotator; this ensures that only the light whose polarization has been rotated by 45° can exit the isolator.

Note that light trying to pass through the optical isolator in the opposite direction would first be polarized to an angle of 45°, and then rotated another 45° by the Faraday rotator (since the rotator is orientation-agnostic). Therefore, the light exiting the rotator in this direction would be polarized orthogonally to the linear polarizer at the other end, meaning that it will be extinguished, and no more light will be reflected back into the ECDL, as desired.

Common choices for nonlinear crystals for use in the Faraday rotator are terbium-doped glass or terbium gallium garnet (TGG) due to their high Verdet constant. Specifically, for the 780nm transition of Rubidium, the Verdet constant of TGG is approximately 60 radians per meter-Tesla. By the above equation, then, to achieve a 45 degree rotation (\(\approx 0.785\) radians), we require \(\approx 0.013\) meter-Teslas.

This can be achieved by a \(15.5\)mm length TGG crystal (purchasing TGG generally requires a custom order from a manufacturer; Chinese manufacturers will produce such a piece for \(\sim\) $80 at the time of writing), and \(19\)mm of permanent toroidal magnets that generate a \(.85\) Tesla axial field at their center (e.g. K&J Magnetics RC44-N52 x 3, $16 and K&J Magnetics R412-N52 x 6, $3).

Optical ‘Pumping’

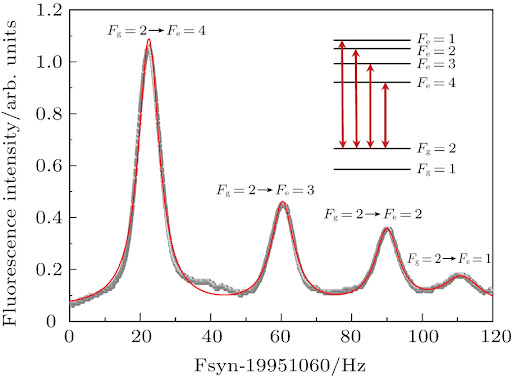
When we utilize the \(780.241\)nm transition of Rubidium-87 to excite atoms in the ground state to the \(5^2 P_{3/2}\) excited state, this corresponds to a \(F=3 \to F'=4\) transition. The \(F'=4\) state must decay back into the \(F=3\) state, meaning that the atoms can be immediately excited once again (and therefore cooled, via the principles of the radiation pressure force). However, due to the phenomenon of Raman scattering, there is a possibility that Rubidium-87 atoms will end up in a hyperfine split \(F=2\) state, which is ‘dark’ with respect to the \(780.241\)nm light.

More generally, all alkali elements are subject to such a phenomenon in one form or another, which typically necessitates the usage of a secondary repumping laser that removes atoms from this ‘dark state’. In Rb-87, this involves an excitation from the \(F=2\) to the \(5^2 P_{3/2}, F'=3\) state, which will then decay back down to \(5^2 S_{1/2}, F=3\), the ground state, making such an atom ready for cooling cycles once again. One favorable property of this particular ‘repumping’ transition in Rb-87 is that it is very close in natural frequency to the cooling transition, being separated by only 6.6GHz. This may be compared to another alkali element, such as Potassium-40, which has a cooling transition at \(405\)nm and a corresponding repumping transition at \(767\)nm, which is a much wider gap.

We may take advantage of this property by generating a sideband in the output beam \(780\)nm ‘cooling’ ECDL that can access this Rb-87 repumping transition. In electromagnetic radiation, a sideband is a band of frequencies that is higher or lower than the main ‘carrier’ frequency, which arises as a result of a modulation process (e.g. voltage controlled oscillation or acousto-optical deflection). In other words, we can modulate the \(780\)nm diode laser such that it will simultaneously generate light at the repumping frequency, so that the experiment can be run with a single ECDL, which greatly reduces both experiment cost and complexity.

Voltage Controlled Oscillators

A cheap and simple implementation of such modulation can be done via the use of a voltage controlled oscillator, or VCO (e.g. Avantek VTO-8240, $55). In particular, for Rb-87 repumping, a microwave oscillator whose range of oscillation is approximately centered about 6.6GHz is optimal. Due to the relatively broad (\(\approx 100\) MHz) line width of the repumping transition, specific details such as harmonic vs. relaxation oscillation and noise figure are not expressly important.

The VCO is a circuit element that can be placed in parallel with the ECDL circuit and a single additional capacitor. It is provided with a separate DC driving voltage, which controls the frequency of oscillation of the VCO. This, in turn, adds an AC voltage source to the circuit that drives a sideband in the laser diode. The input current to a laser diode directly affects its cavity length, which means that this AC modulation will cause a corresponding oscillation in the output frequency of the diode (as the diode’s cavity length directly controls the output frequency of light).

Since the line width of the repumping transition of Rb-87 is relatively large, tuning the DC input to the VCO can be performed (once the remainder of the experiment is correctly set up) by scanning through a range of input voltages until the steady-state MOT is established.

Frequency Locking

Because stable cooling of atoms requires precise control of the frequency of applied light, it is useful (and for robust applications, necessary) to have a method of measuring the frequency of light from our light source. In this section, we present two tools for conducting such measurements: vapor cells and Fabry-Perot interferometers.

Fabry-Perot Interferometry

A Fabry-Perot cavity (or interferometer) is an optical device constructed with two mirrors in a variable-length tube. When operated, light is transmitted through one end of the cavity, and then is reflected back and forth between the two mirrors inside the cavity. The amount of light that is transmitted through the other end of the cavity is dependent on the length of the cavity, due to the variation in the interference patterns of the reflected light inside the cavity with respect to the length.

In particular, after being transmitted through one end of the cavity, the incident light can either be transmitted through the other end, or reflected by the mirror at that end. If the light is reflected, and then once again reflected at the ‘entrance’ to the cavity, it returns to the ‘exit’ of the cavity after some time that is dependent on the refractive index of the material inside the cavity (typically air) as well as the length of the cavity.

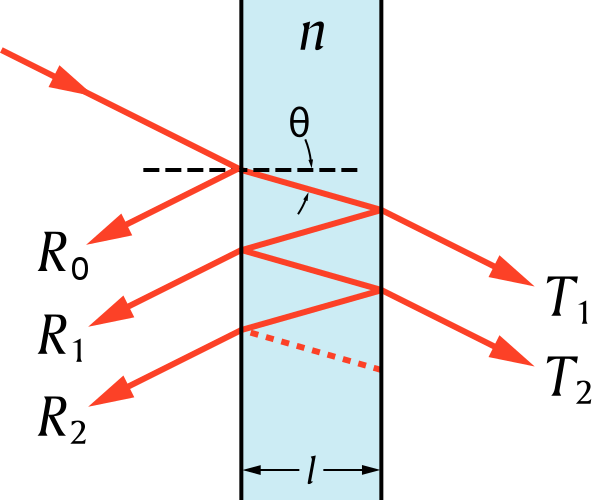
If this reflected light beam is then transmitted, it has a phase difference with the initial transmitted beam that is also dependence on the cavity length and index of refraction. Specifically, if the light is incident at one end of the cavity at an angle of \(\theta\), the phase difference between the first transmitted beam and the beam transmitted after two reflections is given by:

\[\delta = \frac{2 \pi}{\lambda} 2 n \ell \cos \theta,\]

where \(\lambda\) is the wavelength of the incident light, \(n\) is the refractive index of the cavity, and \(\ell\) is the length of the cavity. Moreover, the transmittance of the cavity is given by:

\[T = \frac{(1-R)^{2}}{1-2 R \cos \delta+R^{2}} = \frac{1}{1 + F \sin^2 \frac{\delta}{2}},\]

where \(R\) is the reflectance of the mirrors, and \(F = \frac{4R}{(1-R)^2}\) is the finesse. From these equations, if we take \(n=1\), we can see that transmission is maximized when \(\ell \cos \theta\) is an integer multiple of the wavelength. Therefore, in practice, we direct our light source at the cavity at an angle of \(\theta = 0\), tune the length using a piezoelectric actuator (identical to the one used to tune the ECDL diffraction grating), and place a photodetector at the cavity ‘exit’. Thus, if the initial length of the cavity is known, as we vary the length using the piezo actuator, we can determine the wavelength of the light from the photodetector readings. This can be used as an error signal that then allows us to tune the parameters that determine the frequency of our light source.

Saturated Absorption Spectroscopy

A reliable source of frequency measurement for ground state transitions of atoms is through the usage of atomic vapor cells, which are containers that heat a pure sample of a particular element until it forms a vapor. In an optical experiment, some of the light from the light source can be split off via a beam splitter, directed through such a vapor cell, and then into a photodetector.

Since the majority of the atoms in the vapor cell will be in their ground state, if the light source is emitting at the natural frequency of the cooling transition, the atoms in the vapor cell will be excited (e.g. for Rb-85, into the \(5^2 P_{3/2}\) state). Some proportion of these atoms will spontaneously decay back into the ground state; when this occurs, the emitted photon has a random direction, meaning that it may not hit the photodetector that has been placed in series with the vapor cell.

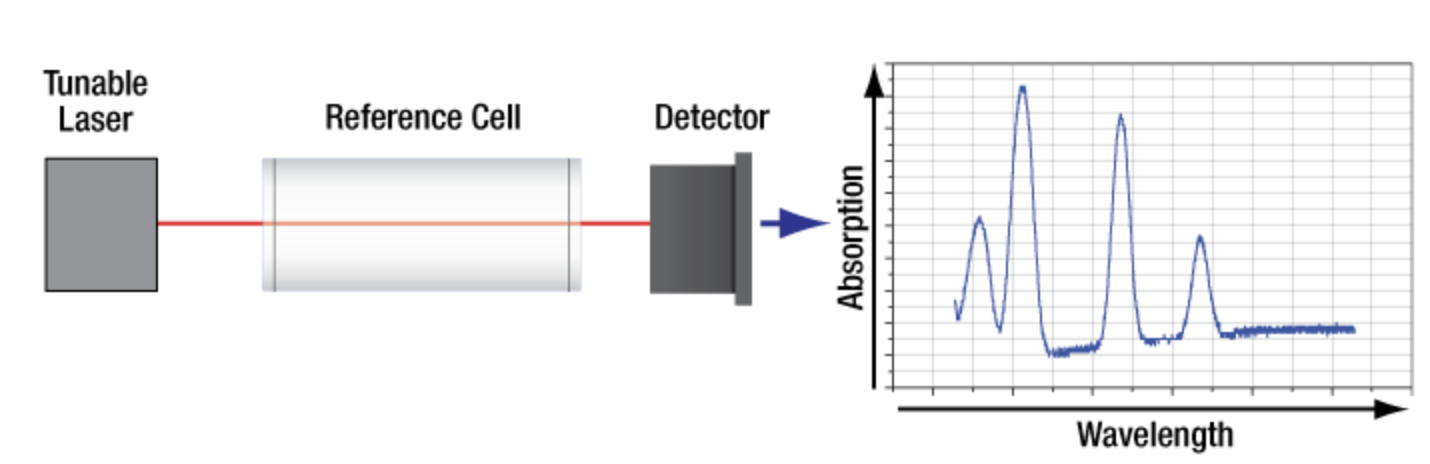
Therefore, when the frequency of the light source is on resonance with the cooling transition, we will see a sharp dip in the absorption measurements from the photodetector, because the light beam is not passing through the vapor straight into the photodetector at that point. This can be used as an error signal, which allows an experimentalist to more precisely tune the parameters of their light source in order to achieve a desired light frequency. Note that atomic vapor cells can only be used as an error signal for ground state transitions, because the vapor cell will only contain atoms in their ground state, and therefore the absorption measurement will only have meaningful fluctuations for transitions that excite atoms from their ground state.